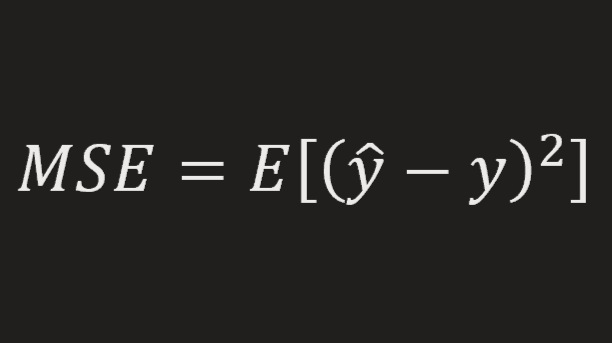School Location Problem

• 

• The Problem

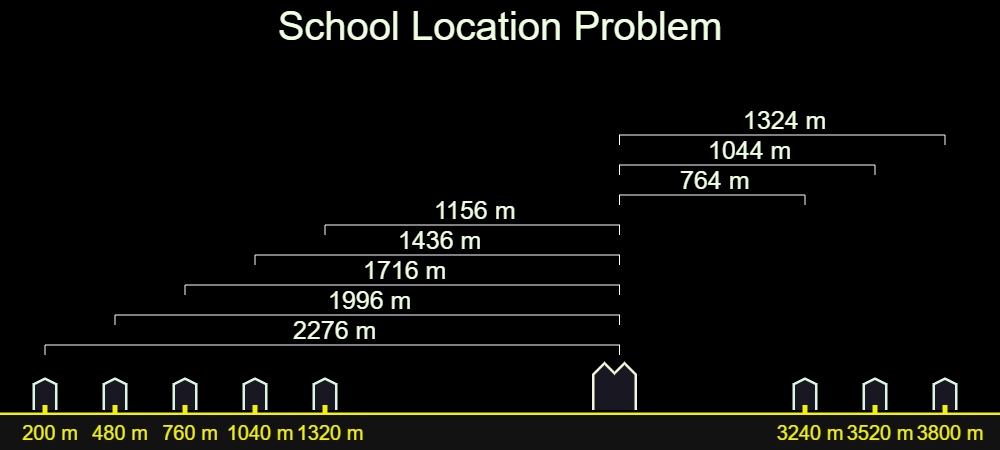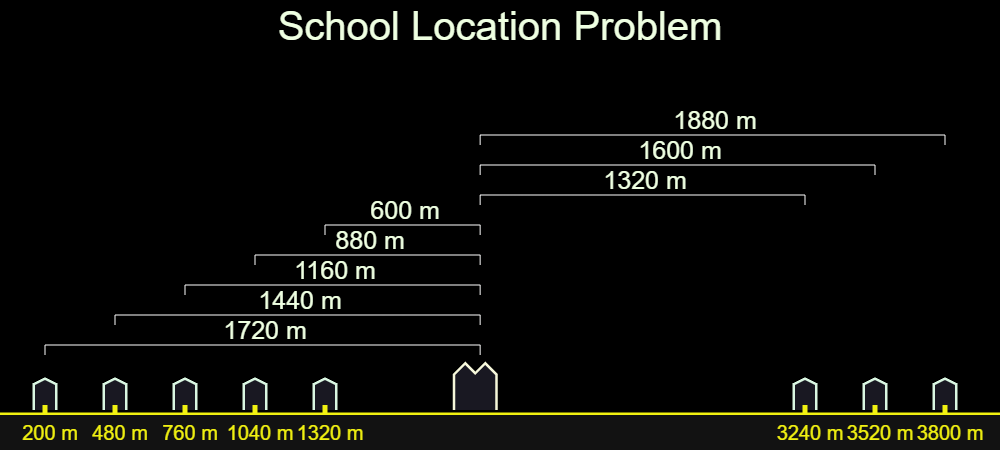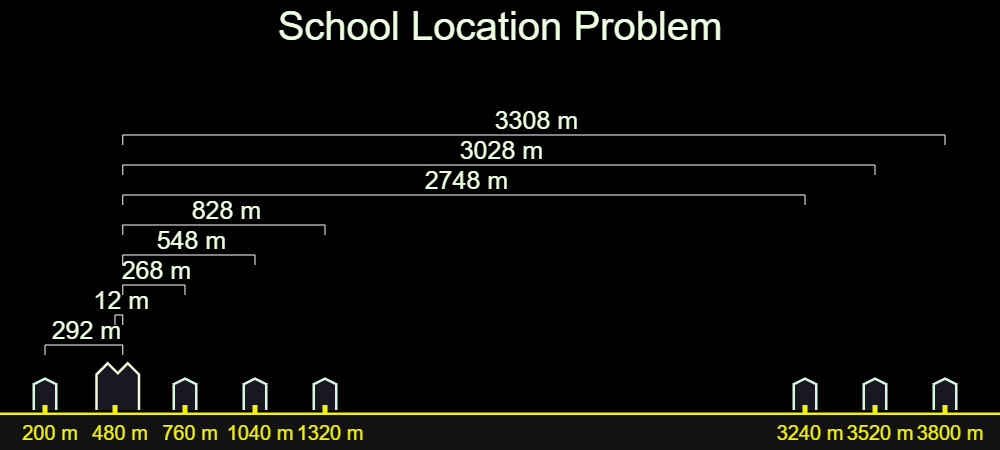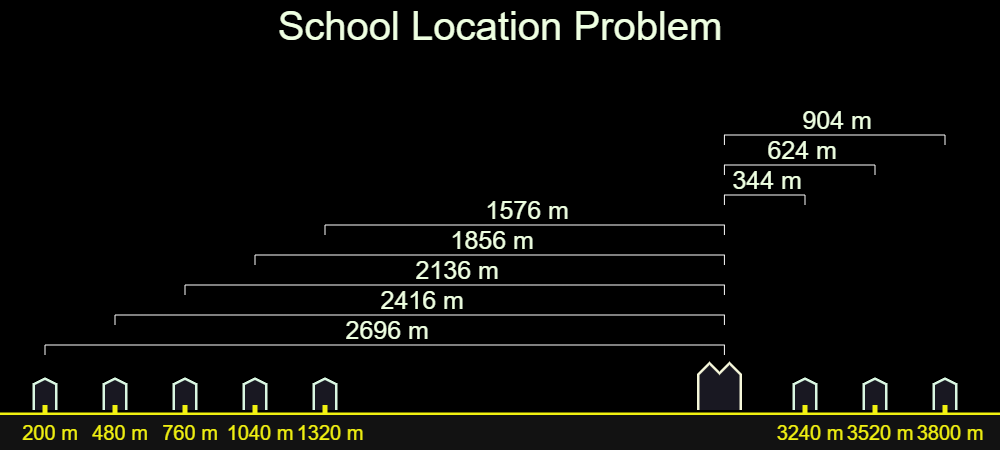
  You are a philanthropist who wants to build a small school in a vast and underpopulated neighborhood. There are 8 children in the neighborhood. Their homes’ distances from the beginning of the road are given below:

  

  You want the sum of distances between the homes and the school is to be minimum. Where should the school be built?

  The Answer

  You may think that the school should be in a central position, such as average of distances of homes from the beginning of the road. Would you like to see different cases? Here below is an interactive widget to see the possible situations.

  For desktop: Hover your mouse over the image below
  For mobile: Click the image below

  If you tried, you probably noticed that between 4th and 5th homes total distance at its minimum (9400 m). Briefly, the answer is median.

  

  The Solution

  But how? Let’s formulate the problem.

   

  • \(h_i\): Distance of the home ifrom the beginning of the road.
  • \(s\): Distance of the school from the beginning of the road.

  hivalues are already given. We should choose svalue which minimizes total distances. The distance between sand any hican be shown with absolute value of their differences:

  \(|h_i-s|\)

  So we want total of the distances Dto be minimum:

  \(D = \displaystyle\sum_{n=1}^{8}|h_i-s|\)

  or more explicitly:

  \(D=|h_1−s|+|h_2−s|+|h_3−s|+|h_4−s|+|h_5−s|+|h_6−s|+|h_7−s|+|h_8−s|\)

  If the expression were differentiable, we would simply find its derivative and equate it to zero to find the s. However, absolute functions prevent that. Still we can try to find the minimum value.

  For \(|h_i-s|\), we know that:

  • If \(|h_i-s| > 0\) then \(|h_i-s| = h_i-s\)
  • If \(|h_i-s| < 0\) then \(|h_i-s| = -(h_i-s)\)
  • If \(|h_i-s| = 0\) then \(|h_i-s| = 0\)

  And also we know that:

  \(h_1<h_2<h_3<h_4<h_5<h_6<h_7<h_8\)

  
  Thus, for \(s<h_1\):

  \(D=(h_1−s)+(h_2−s)+(h_3−s)+(h_4−s)+(h_5−s)+(h_6−s)+(h_7−s)+(h_8−s)\)

  \(D=h_1+h_2+h_3+h_4+h_5+h_6+h_7+h_8−8s\)

  \(D=14360−8s\)

  
  For \(h_1≤s<h_2\):
  \(D=−(h_1−s)+(h_2−s)+(h_3−s)+(h_4−s)+(h-5−s)+(h_6−s)+(h_7−s)+(h_8−s)\)

  \(D=−h_1+h_2+h_3+h_4+h_5+h_6+h_7+h_8−6s\)

  \(D=13960−6s\)

  
  For \(h_2≤s<h_3\):
  \(D=−(h_1−s)−(h_2−s)+(h_3−s)+(h_4−s)+(h_5−s)+(h_6−s)+(h_7−s)+(h_8−s)\)

  \(D=−h_1−h_2+h_3+h_4+h_5+h_6+h_7+h_8−4s\)

  \(D=13000−6s\)

  Below is a graph shows Daccording to different values of s. It consists of combination of lines with different slopes. You can see the equations of the lines on the graph.

  

  As you can see, the graph has a “U” shape .The slope of \(D\) falls and then rises as \(s\) increases. In the case that \(s\) is between 1040 (\(h_4\)) and 1320 (\(h_5\)), \(D\) is at its minimum value. Thus, the median, which is \(\frac{h_4+h_5}{2}\), is also one of the answers. Fun fact: the derivative of \(D\) is zero only between \(h_4\) and \(h_5\).

  You can change the positions or number of the homes. The result will always include the median. If number of homes is odd, then the minimum distance can only be provided by the median.

optimization