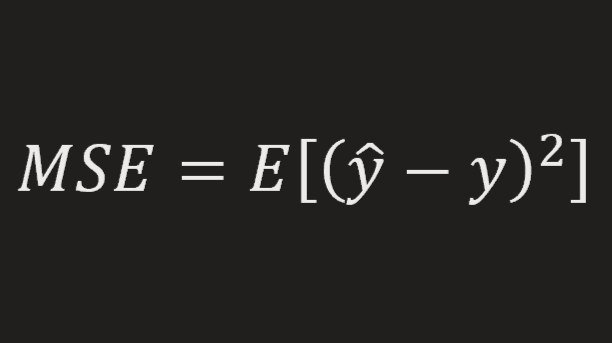Generating Populations with Given Mean and Variance
-
-
-
Can you easily generate a population whose mean and variance are given? Yes you can! You don’t even have to write any piece of code. In this post, I will explain how to do it with a discrete uniform distribution.
Uniform Distribution
A discrete uniform distribution consists of equally possible outcomes. For instance, outcomes of rolling a fair die have a uniform distribution. Each of the outcomes (1,2,3,4,5,6) has probability of 1/6.
However, total of two fair dice does not have a uniform distribution. High and low values are less probable.
If you want to learn more about discrete uniform distributions, you can check out RandomServices’ article.
Distribution Formula
We can define a uniform distribution by its minimum value (\(a\)), population size (\(n\)), and and step size (\(h\)):
Our population can be shown like this:
\([a,a+h,a+2h,…,a+(n−3)h,a+(n−2)h,a+(n−1)h]\)
So we can describe any element (\(x\)) of our population (\(X\)) as:
\(x_i=a+(i−1)h\)
I think it will probably be handy if we describe \(x_i\) in terms of the mean (\(m\)) of the population instead of \(a\). But how? Let’s try something different. Here is the reversed version of our population:
\([a+(n−1)h,a+(n−2)h,a+(n−3)h,…,a+2h,a+h,a]\)
Calculating element-wise addition of the original and reversed versions of the population, we get a new one:
\([2a+(n−1)h,2a+(n−1)h,…,2a+(n−1)h,2a+(n−1)h]\)
Each element of the new population is \(2a+(n−1)h\), which is also the mean. We also know that this population’s mean is twice the mean of our original population. Thus, the mean of our original population should be \(a+\frac{(n-1)h}{2}\). So we can formulate \(a\) as:
\(a=m-\frac{(n-1)h}{2}\)
According to this, we can reformulate xias:
\(x_i=m-\frac{(n-1)h}{2}+(i−1)h\)
Finding Parameters
We want to generate a population with predefined mean and variance values. What we have are three controllable parameters: \(a\), \(n\), and \(h\). Let’s analyze how mean and variance change by some transformations.
Changing ameans moving each item of the population. If we do that, the mean changes but the variance is not affected:
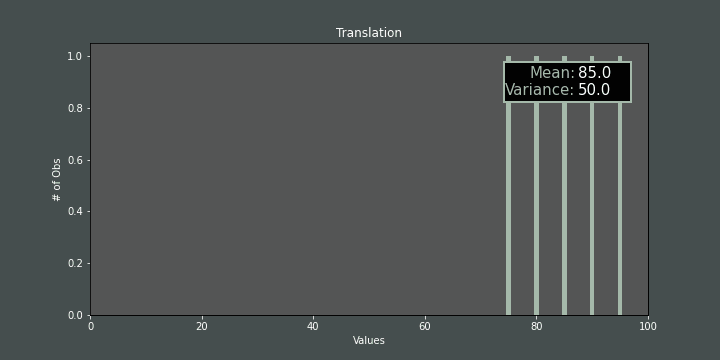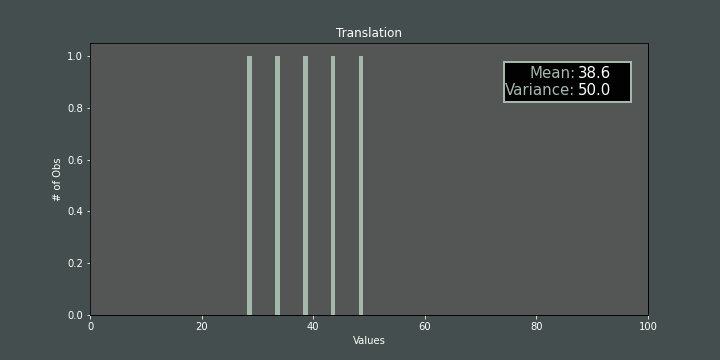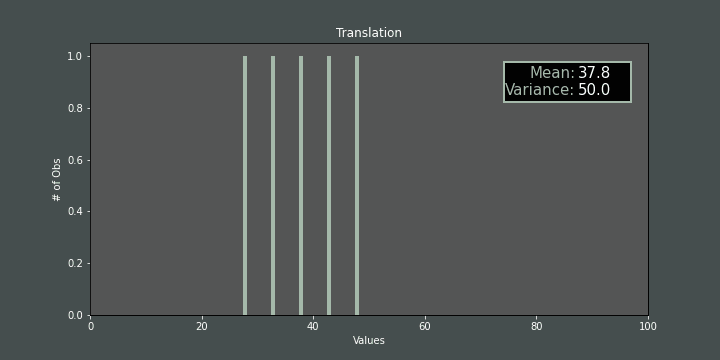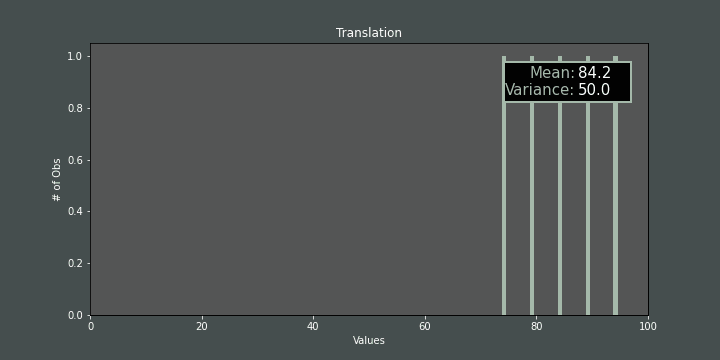
If we change step size (\(h\)) while mis fixed, the variance also changes accordingly:
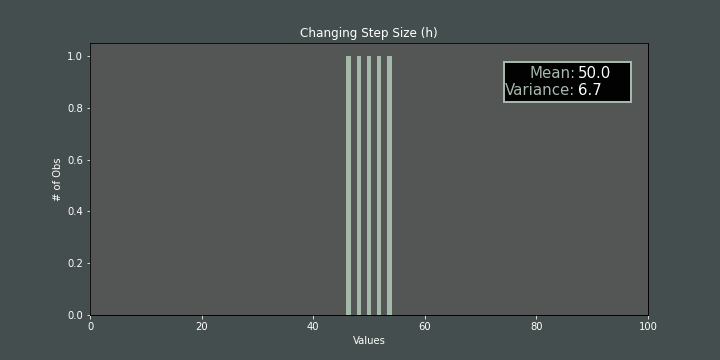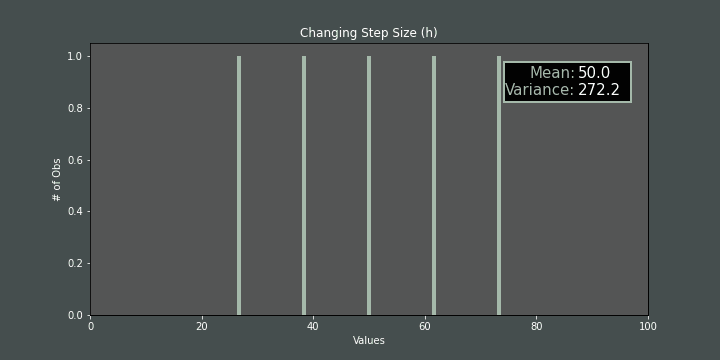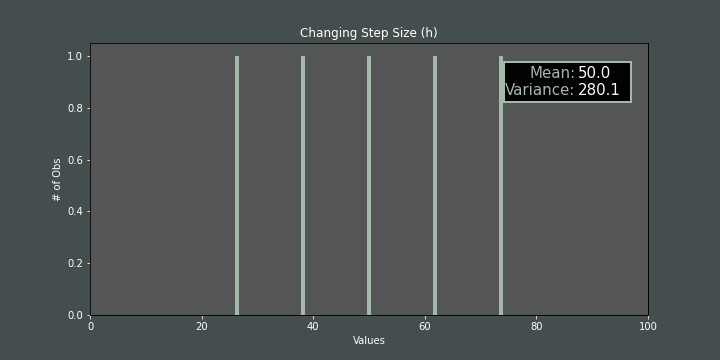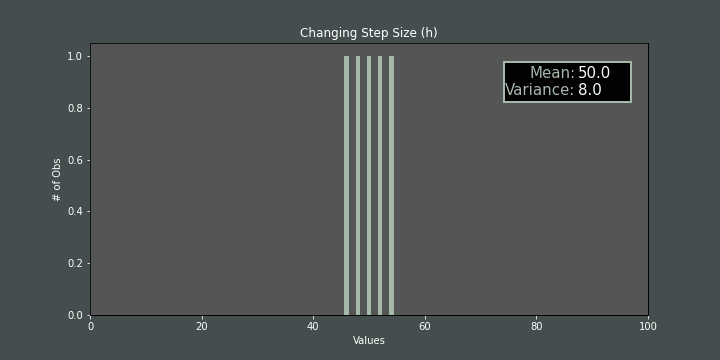
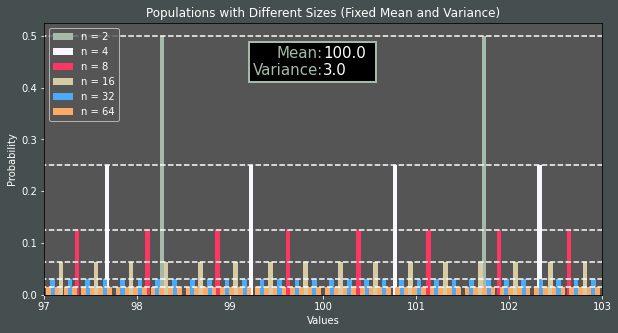
If we increase/decrease the number of items while mand hare fixed, again, the variance is affected:
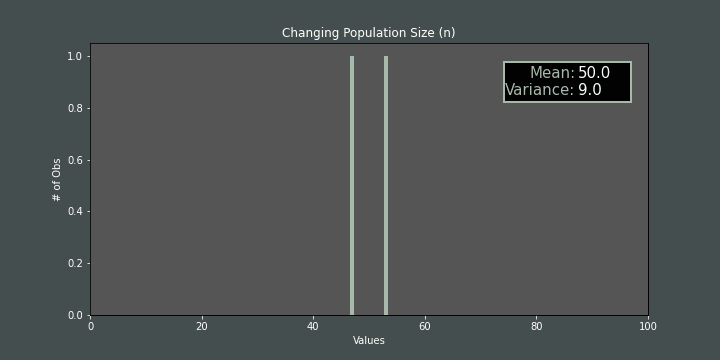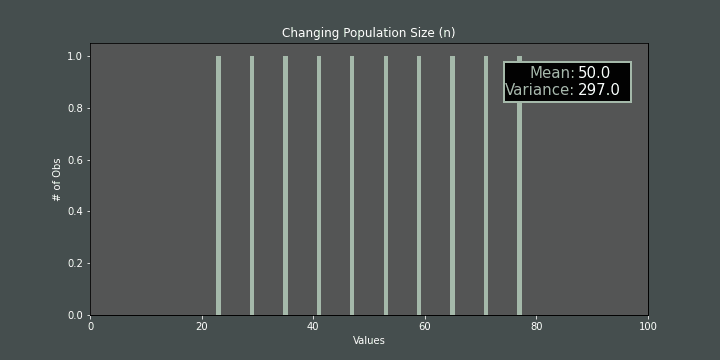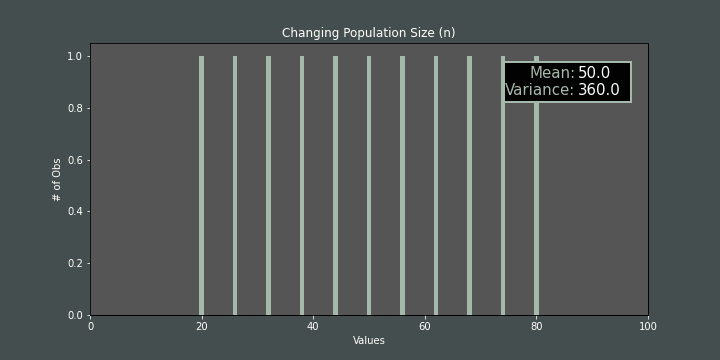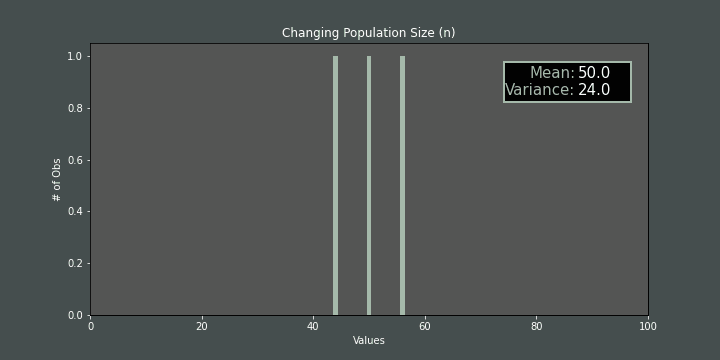
So we can conclude that if we fix the mean to the predefined mean value, we just need to find the right \(n\) and \(h\) values to have the desired variance value (\(σ^2\)). The relationship among step size (\(h\)), population size (\(n\)) and variance (\(σ^2\)) is shown below:
\(h=\sqrt\frac{12\sigma^2}{n^2-1}\)
Here is the explanation of how the formula is derived:
The standard variance formula is:
\(\sigma^2 =\frac{ \displaystyle\sum_{i=1}^n(x_i-m)^2}{n}\)
Since we know the formula of \(x_i\):
\(\sigma^2 =\frac{ \displaystyle\sum_{i=1}^n[m-\frac{(n-1)h}{2}+(i−1)h-m]^2}{n}\)
\(m\) values cancelled each other out. The rest of the terms in sum of squares have \(h\) as multiplier. Thus, we can take \(h\) out of the summation as \(h^2\):
\(\sigma^2 =\frac{h^2}{n} \displaystyle\sum_{i=1}^n[-\frac{n-1}{2}+(i−1)]^2\)
We expand the squared terms in summation:
\(\sigma^2 =\frac{h^2}{n} \displaystyle\sum_{i=1}^n[(\frac{n-1}{2})^2-(n-1)(i-1)+(i−1)^2]\)
The summation can be separated into three parts as below:
\(\sigma^2 =\frac{h^2}{n} [ \displaystyle\sum_{i=1}^n(\frac{n-1}{2})^2 -\displaystyle\sum_{i=1}^n(n-1)(i-1) +\displaystyle\sum_{i=1}^n(i−1)^2 ]\)
We can calculate the summations by sum of series formulas:
\(\sigma^2 =\frac{h^2}{n} [ \frac{n(n-1)^2}{4} -\frac{n(n-1)^2}{2} +\frac{n(n-1)(2n-1)}{6} ]\)
The rest is just simple algebra:
\(\sigma^2 = h^2(n-1)[\frac{n-1}{4}-\frac{n-1}{2}+\frac{2n-1}{6}]\)
\(\sigma^2 = h^2(n-1)[\frac{n+1}{12}]\)
\(\sigma^2 = h^2\frac{n^2-1}{12}\)
\(h=\sqrt\frac{12\sigma^2}{n^2-1}\)
Try It Out
Let’s assume that you want to create a population whose mean is 100 and variance is 6. You just need to choose a population size and apply the formulas. If you want the number of items to be 3, then the step size must be:
\(h=\sqrt\frac{12*6}{9-1}=3\)
And from previous calculations, we know that:
\(a=100-\frac{(3-1)3}{2} = 97\)
So each item of our population can be found as below:
\(x_i = a+(i-1)h = 97+(i-1)3\)
Thus, our population is:
[97,100,103]
It is worth noting that we can select any whole number bigger than 1 as the population size. Here are the other options for the same mean and variance values: