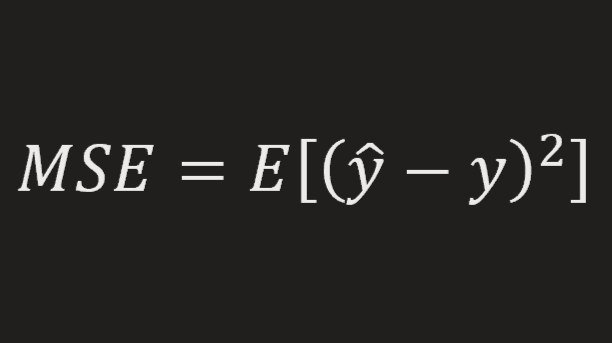KL Divergence (Normal Dist vs Standard Normal Dist)
-
-
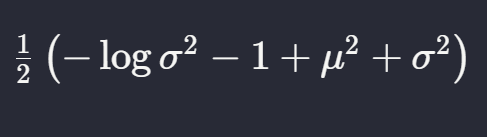
-
Variational Autoencoders (VAEs) are very popular due to their abilities in data generation. A classic VAE model has two terms in its loss function: reconstruction error and KL-divergence. While the first term provides a similar output for the given input, the second term approximates the made-up posterior to the prior.
In general, this KL-divergence term formulated as below:
\(\frac{1}{2}\left( -\log{\sigma^2}-1+\mu^2+\sigma^2 \right)\)
The ones who applied method without knowing the details might not be aware but it is not a random formula. In VAE, we try to make our approximated posterior \(q_{\phi}(z|x)\) as close as possible to the prior \(p_{\theta}(z)\). In most convenient configuration, posterior is assumed to follow normal distributions with a mean \(\mu\) and standard deviation \(\sigma\) while the prior is a standard normal distribution.
\(q_{\phi}(z|x) \sim N(\mu,\sigma^2)\) \(p_{\theta}(z) \sim N(1,0)\)
The KL-divergence between this two distribution becomes:
\(KL(q_{\phi}(z|x) \Vert p_{\theta}(z))\)
\(= E_{q_{\phi}(z|x)}\left[\log q_{\phi}(z|x)\right]-E_{q_{\phi}(z|x)}\left[\log p_{\theta}(z) \right]\) (1)
\(= E_{q_{\phi}(z|x)}\left[\log \frac{1}{\sqrt{2\pi}\sigma}\exp{-\frac{(z-\mu)^2}{2\sigma^2}} \right]-E_{q_{\phi}(z|x)}\left[\log \frac{1}{\sqrt{2\pi}}\exp{-\frac{z^2}{2}} \right]\) (2)
\(= E_{q_{\phi}(z|x)}\left[\log \frac{1}{\sqrt{2\pi}\sigma} \right]+E_{q_{\phi}(z|x)}\left[-\frac{(z-\mu)^2}{2\sigma^2} \right]-E_{q_{\phi}(z|x)}\left[\log \frac{1}{\sqrt{2\pi}} \right]-E_{q_{\phi}(z|x)}\left[-\frac{z^2}{2} \right]\) (3)
\(= \log \frac{1}{\sqrt{2\pi}\sigma}+E_{q_{\phi}(z|x)}\left[\left(-\frac{(z-\mu)}{2\sigma}\right)^2 \right]-\log \frac{1}{\sqrt{2\pi}}-E_{q_{\phi}(z|x)}\left[-\frac{z^2}{2} \right]\) (4)
\(= -\frac{\log{\sigma^2}}{2}-\frac{E_{q_{\phi}(z|x)}\left[\left(\frac{(z-\mu)}{\sigma}\right)^2 \right]}{2}+\frac{E_{q_{\phi}(z|x)}\left[z^2 \right]}{2}\) (5)
\(= -\frac{\log{\sigma^2}}{2}-\frac{\left(E_{q_{\phi}(z|x)}\left[\frac{(z-\mu)}{\sigma} \right]\right)^2}{2}-\frac{Var_{q_{\phi}(z|x)}\left[\frac{(z-\mu)}{\sigma} \right]}{2}+\frac{\left(E_{q_{\phi}(z|x)}\left[z \right]\right)^2}{2}+\frac{Var_{q_{\phi}(z|x)}\left[z \right]}{2}\) (6)
\(= -\frac{\log{\sigma^2}}{2}-\frac{1}{2}+\frac{\mu^2}{2}+\frac{\sigma^2 }{2}\) (7)
\(= \frac{1}{2}\left( -\log{\sigma^2}-1+\mu^2+\sigma^2 \right)\) (8)